CVPR2019 物体検出の論文紹介 Anchor系編

文献紹介

CVPR2019 物体検出論文紹介 Anchor系編 はじめまして、CTO室の毛利です。
弊社では毎年、画像処理・機械学習の国際会議に参加しております。 昨年は、私ともう1名でカリフォルニアのロングビーチで行われたInternational Conference on Machine Learning(ICML)とConference on Computer Vision and Pattern Recognition(CVPR)とに参加してきました。

今回から2回に分けて、CVPR2019で発表された物体検出の論文の中で、私が面白いと思ったものを紹介したいと思います*1。 初回では、はじめに物体検出の概要を説明し、次いでAnchor系の論文の紹介をします。 基本的に手法を中心に紹介し、実験結果については簡単な言及にとどめるので、気になった方は原論文を参照ください。

物体検出の概要

まず、物体検出の概要について説明します。 かなり駆け足で説明しているので、Deep Learningを用いた物体検出の知見が無い方は、FasterRCNN, SSDなどの有名な手法を事前に理解しておいた方がいいと思います。

物体検出は、画像に写った物体の種類と位置(矩形で指定)を特定するタスク:

  • 入力: 画像
  • 出力: 画像に写った各物体の 種類(クラス), 矩形位置, 対象の種類である確率(スコア)
    物体検出の結果例。物体の種類・位置に加えて、その種類の物体である確率も出力する。

データセット

  • 昔はPASCAL VOCがよく使われていたが、今はMS COCOがスタンダード
  • PASCAL VOCとMS COCOで標準の評価指標が違う(次節で説明)

評価指標: mean Average Precision(mAP)

  • 推論矩形と正解矩形(Ground Truth, GT)の重なり度合い(Intersection over Union, IoU)から正解かどうかを判定する。推論はあるしきい値以上のスコアの出力を使う。したがって、検出成功の判定はIoUのしきい値、スコアのしきい値で変化する。
    • True Positive(TP): 推論結果とGTのIoUが一定(例えば0.5)以上
    • False Positive(FP,誤検出): 重なるGTがない推論
    • False Negative(FN,未検出): 重なる推論がないGT
      コップの検出結果。 例として、スコアのしきい値を0.5に設定したとする。 右のスプレーボトルは、コップではないのにコップとして推論してしまっているために誤検出(False Positive)になる。 真ん中のコップは、推論結果(青枠)のスコアが低いために未検出(False Negative)になる。 左のコップは、正解(赤枠)との重なりが小さめである。IoUがしきい値以上の場合はTrue Positiveになり、IoUがしきい値以下の場合にはFalse NegativeかつFalse Positiveになる。
  • 検出率(Recall)と精度(Precision)を以下で定義する:
\begin{aligned} \mathrm{Recall} &= \frac{TP}{TP+FN} = \frac{TP}{\mathrm{\#GT}} \\ \mathrm{Precision} &= \frac{TP}{TP+FP} = \frac{TP}{\mathrm{\#Deteced}} \end{aligned}
  • PRカーブ(スコアのしきい値を変化させた時にできるRecall vs Precisionの曲線)の下の面積(Area Under the Curve, AUC)をAverage Precision(AP)と呼ぶ(APはクラスごとに定義される)
  • 各クラスのAPを平均したものをmean AP(mAP)と呼ぶ
  • PASCAL VOCではIoUのしきい値を0.5とした場合のmAPを評価指標として使う。
  • MS COCOではIoUのしきい値を[0.5, 1]の範囲で変えてmAPを平均する。つまり、PrecisionをIOU，クラス、Recallに関して平均したものを評価指標として使う(そういう意味では、mean mean average precisionと呼ぶべきかも知れないが、これも"mAP"と呼ばれる)。

手法の分類

現在使われているDeep Learningを用いた物体検出は、大きくは以下の2種類に分けられる。 2018年にCornerNetが提案されて以降、Heatmap系の手法が主流になりつつある。

  • Anchor系
    基準となる矩形(Anchor, Prior, Default boxなどと呼ばれる)を規則的に大量に並べて、Anchor boxがどのクラスになるか、物体の場所がAnchor boxからどれくらいズレているを推論する。 さらに、以下の2種類に分けられる。
    • one-stage系(高速)
      • Anchorからいきなりクラスと位置のズレを推論する
      • 例: SSD, YOLO, RetinaNet
    • two-stage系(高精度)
      • 候補となる矩形をまず推論させて、その候補からクラスと位置のズレを推論
      • 例: R-CNN, Faster-RCNN, Mask-RCNN, M2Det
  • Heatmap系 (世間的にはAnchor-free系と呼ばれる)
    矩形の座標をheatmapで推論する
    • 例: CornerNet, FCOS, FSAF, CenterNet(同じ名前の別の手法が2つあるので注意)
    • 2018年にCornerNetが提案されて以降、Heatmap系の手法がたくさん提案されている（CVPR2019ではAnchor系とHearmap系で半々くらいだった）

Anchor系の手法概要

  • 決まった大きさ・アスペクト比のAnchor boxを等間隔に並べる。 各Anchor boxが(背景を含めた)どのクラスになるかの分類 + Anchor boxの位置を基準としたregressionをすることで物体を検出する。
    サイズ6x3(アスペクト比2:1)で、間隔4のAnchorの例
  • One-stage系のネットワーク構造例
    Classificationで使われるResNetやMobileNetなどのCNNをBackboneとして、特徴量を取り出す。 元解像度の1/4 x 1/4の解像度の特徴量であれば、Anchor boxの間隔は4になる。 Backboneの特徴量を入力としたSubNetworkで、各AnchorのClassification(背景を含める)と、Anchorの位置を基準としたregressionを行う。
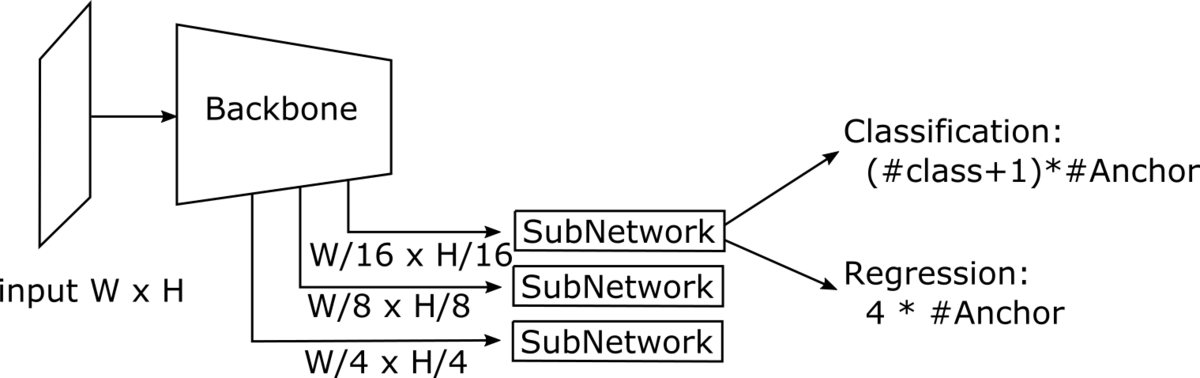
  • 一つの正解矩形に対して、ネットワークの出力は複数の矩形が対応する場合がある。そこで、冗長な出力を削るために、一定以上の重なりになる矩形はスコアが大きいものだけを残すという処理(Non Maximum Suppression, NMS)をする。

Y. He et al, "Bounding Box Regression With Uncertainty for Accurate Object Detection" (2018)

  • Anchor系の手法は、Anchor boxのclassificationとregressionという2つのタスクに分けられるが、この論文はregression部分の精度向上を試みた
  • 普通、regressionは矩形の位置のみを予測するが、位置に加えて位置の不確実性も予測する手法を提案
  • さらに、矩形の位置の不確実性をNMSの時に使って、矩形位置を補正する後処理も提案

モチベーション

  • 物体検出のデータセットでは、以下のような不適切なGT(正解データ)が含まれる。このデータでregressionを学習すると悪影響がある。
    • GTの矩形位置が不正確: 下図のa,cでは、いずれも本当の正解より小さめの矩形になってしまっている
    • 隠れによって原理的に物体境界が決まらない: 下図のb,dでは、物体の左端が隠れによってどこか分からない
      学習に悪影響のあるAnnotationの例。[He+(2018)] Figure 1 より引用
  • classificationのスコアとregressionの正確さは必ずしも一致しない。 普通、一つの同じ物体に対してネットワークは複数の推論矩形を出力するので、NMSで一つだけ選択する。 下図の例は、一つの物体に対してネットワークが出力した推論矩形の例で、NMSではclassificationスコア(矩形左上の数字)が高い矩形が採用される。 下図の例では、classificationスコアが高い矩形の位置が必ずしも正確ではない(右下図の鳥の左辺のように、スコアが低い矩形の方が位置が正確な場合がある)。
    classificationのスコアとregressionの正確さが一致しない例。[He+(2018)] Figure 2 より引用
  • 矩形の位置の信頼度が推論できれば、後処理(自動運転やロボティクスなどの応用時)で使える

手法: KL loss

既存手法: 矩形位置のみ予測

  • regression target t_x, t_yは、左上と右下の座標 x, yを以下のようにエンコードしたもの:
\begin{aligned} t_x &= \frac{x-x_a}{w_a} \\ t_y &= \frac{y-y_a}{h_a} \end{aligned}

ここで、 x_a, y_aはanchor boxの位置、 w_a, h_aはanchor boxの幅・高さ。

  • 既存手法では t_x, t_yを推論させ、(smooth) l_{1}-lossでregressionの学習を行う。

提案手法: 矩形位置に加えて、その不確実性を予測

  • この論文が提案しているKL lossでは、矩形位置の確率分布を推論させる。確率分布は単純なガウス分布でモデル化する:
\begin{aligned} P_{pred}(t) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(t-t_{pred})^2}{2\sigma^2}} \end{aligned}

ここで、 t_{pred}が推論したregression targetの値で、 \sigmaが推論結果の不確実性を表す。左上と右下の座標を推論したいので、これが4つ(左上、右下のx,y)ある。

  • GTの確率分布はDiracの \delta-関数と仮定する(ガウス分布で \sigma\to\inftyの極限をとったもの):
P_{GT}(t) = \delta(t-t_{GT})
  • これらの確率分布を近づけたいので、確率分布間の距離を表すKL-divergenceをLoss(KL-loss)として使う:
    • これは、不確実性を \sigma=1 に固定した時には、普通の l_2-lossに帰着する。
    • 推論 t _ {pred} が GT t _ {GT} に近い時は \sigmaを小さくした方が良く、遠い時は \sigmaを大きくした方がよい。
    • 逆に考えると、ネットワークが難しいと判断した場合(隠れで物体境界が曖昧な場合など)は不確実性 \sigmaが大きくなり、矩形位置 t _ {pred}はあまり学習されない。実際、隠れで物体境界が曖昧な場合は、どこに境界を設定してもある意味正解なので妥当そう。
\begin{aligned} \mathcal{L}_{reg.} &= D_{KL}(P_{pred}(t)||P_{GT}(t))\\ &\propto \frac{(t_{pred}-t_{GT})^2}{\sigma^2} + \log{\sigma^2} \end{aligned}

  • Classification・矩形位置に加えて、矩形位置の不確実性に関係する \sigma^ 2を推論するSubNetworkを追加する(下図)
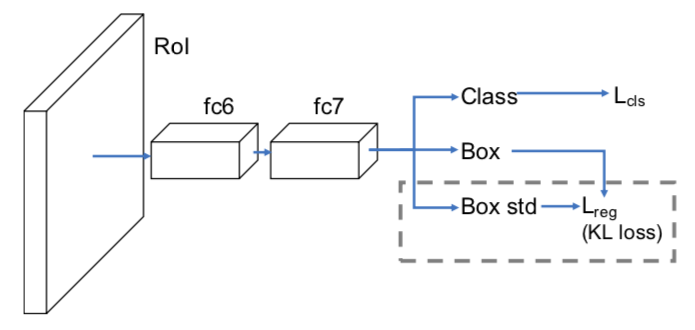
    SubNetworkの構造。[He+(2018)] Figure 3 より引用
  • 補足
    • 今回は独立ガウス分布を確率分布として使ったが、より複雑な分布(共分散が対角的でないガウス分布や、混合ガウス分布など)を用いてもよい
    • 数値的な安定性のために \sigmaそのものでなく、 \alpha:=\log\sigma^ 2を推論させる: \mathcal{L} _ {reg.} = e^ {-\alpha}(t _ {pred}-t _ {GT})^ 2 + \alpha
    • 外れ値に対してロバストになるように、 |t _ {pred}-t _ {GT}|>1の時には l_1-lossを採用する: \mathcal{L} _ {reg.} = 2e^{-\alpha} |t _ {pred}-t _ {GT}-1/2| + \alpha
      • 不確実性を使わない既存手法でも、こういったロバストなlossが使われるので、自然な変更

    • 手法: variance voting

    • classificationのスコアが低くても、regressionの不確実性が低い( \sigmaが小さい)矩形の位置を反映させるために、NMSの際に矩形の位置を修正する
    • 採用する矩形と重なっている矩形の位置を重み付き平均する:
      • 重みはIoUが大きいほど大きく、不確実性 \sigma_{t_i}が大きいほど小さくする
      • classificationスコアは矩形のrefineでは使わない (矩形の正確さとはあまり関係がないので)
    \begin{aligned} t &= \frac{\sum_i w_i t_i}{\sum_i w_i} \\ \\ s.t. \ \ \ w_i &= \frac{e^{-(1-IoU(b_i, b))^2/\sigma_t}}{\sigma_{t_i}^2} \end{aligned}
    • variance votingの結果例
      下図は上段がネットワークの推論矩形で、白枠が分類スコア・緑枠が不確実性 \sigmaの値。
      下段が重なっている矩形を使ってvar votingで修正したもので、分類のスコアが低くても、regressionの不確実性が低ければ矩形の位置に寄与している。

    variance votingの結果例。[He+(2018)] Figure 5 より引用

    実験

    • KL loss、variance votingともに精度向上に寄与する
    • variance votingはSoftNMSと組み合わせて使うことも可能で、両方使うと一番精度が良い

    感想・コメント

    • regressionの出力に不確実性を加えるという方法はDetectionに限らず、一般のregressionに使えそう
      • 不確実性の正解データは必要ない (あってもいいが)
    • KL lossを使うと、GTも間違っているようなサンプルは \sigmaが大きくなるのでregressionはあまり学習されず、 \sigmaが小さくなる信頼できるデータをより学習するようになりそう。 ただし、GTの完全にランダムな"ノイズ"に対しては意味がない。隠れがある場合のように、画像からGTが間違っている可能性が予想できるようなものでないと効果がない。

    H. Rezatofighi et al., "Generalized Intersection Over Union: A Metric and a Loss for Bounding Box Regression" (2019)

    • 評価の際に使われる矩形間の"距離"(IoU)と、学習時にlossとして使われる矩形間の"距離"のミスマッチを解消した

    モチベーション

    • 評価の際の、正解矩形と推論矩形の近さの指標にはIntersection over Union(IoU)は使われる
    • 一方、学習時のregression lossとしては、普通 (smooth-) l_1 や l_2ノルムが使われる
      • 矩形の右上と左下の座標(をエンコードしたもの)を推論する場合と、矩形の中心と幅高さ(をエンコードしたもの)を推論する場合がある
    • IoUと l_nノルムは別物なので、 l_nノルムの値が同じでも、下図の例のようにIoUは大きく違うことがある。
      • 黄緑枠が正解矩形、黒枠が推論矩形を表す
      • (a)は矩形の右上と左下の座標を推論する例で、3つの例で推論矩形と正解矩形の間の l_2ノルムは全く同じ値だが、IoUは大きく違う
      • (b)は矩形の中心と幅高さを推論する例で、3つの例で l_1ノルムは全く同じ値だが、IoUは大きく違う

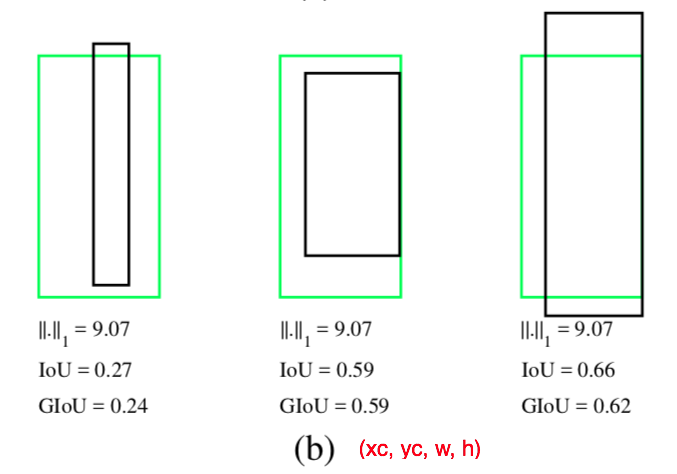
    IoUと l_nノルムの比較。[Rezatofighi+(2019)] Figure 1 より引用

    • そこでIoUをlossとして使いたいが、GTとpredictionが重なっていない時には常にゼロになってしまうという弱点がある

    IoUの性質

    • 👍 l_nノルムはスケール不変でないが、IoUはスケール不変である。 具体的には、スケール倍した座標系での矩形\bar{A}, \bar{B}のIoUは、元の座標でのIoUと一致する：
    \mathrm{IoU}(A, B) = \mathrm{IoU}(\bar{A}, \bar{B})

    ※ l_nノルムは単純にはスケール不変ではないが、lossとして使う場合にはanchorサイズで正規化することで、Heuristicにスケール不変っぽくするのが普通

    • 👍 IoU loss \mathcal{L}_{\mathrm{IoU}} := 1-\mathrm{IoU}は"距離"の定義を満たす（GTとpredictionの"遠さ"を測る指標になる）:

      • 非負: \mathcal{L} _ {\mathrm{IoU}} \geq 0
      • \mathcal{L} _ {\mathrm{IoU}}(A,B) = 0 \Leftrightarrow A = B
      • \mathcal{L} _ {\mathrm{IoU}}(A,B) = \mathcal{L} _ {\mathrm{IoU}}(B,A)
      • 三角不等式: \mathcal{L} _ {\mathrm{IoU}}(A,C) \leq \mathcal{L} _ {\mathrm{IoU}}(A,B) + \mathcal{L}_{\mathrm{IoU}}(B,C)

    • 👎 重なりがない時に常にゼロになる（勾配もゼロで学習されない） → Generalized IoUで解決

    Generalized IoU (GIoU)

    • GIoUは、AとBを含む最小の矩形Cを使って以下のように定義される：

      [Rezatofighi+(2019)] Algorithm 1 より引用

    • 👍 GIoUはIoUの持っている良い性質（スケール不変・距離の定義）を持つ

    • 👍 GIoUはIoUと違って、矩形間の重なりがない時にも値が変化する
      • IoUもGIoUも、微分可能なのでlossとして使える
      • IoUは重なっていないときには常にゼロで勾配がないので学習されないが、GIoUは重なっていない時にも勾配が変化するので学習される
    • IoUが大きい時にはGIoUとほぼ一致し、IoUが小さい時(重なっていない時を含む)には割と異なる(下図)

    [Rezatofighi+(2019)] Figure 2 より引用

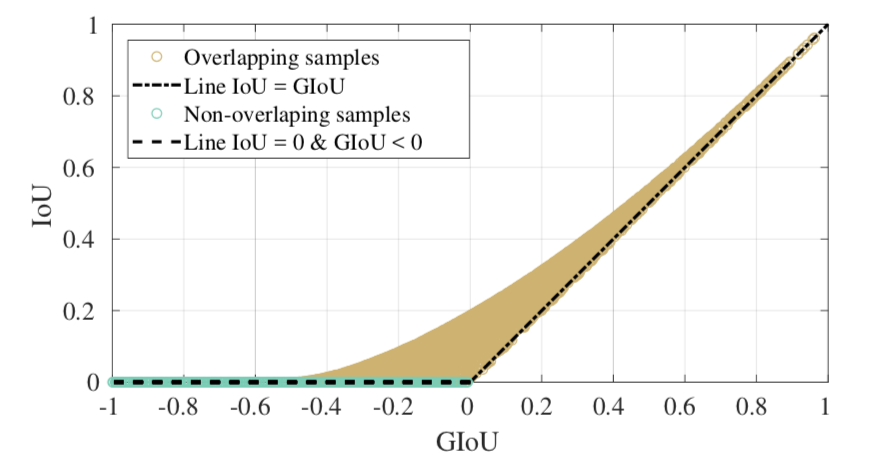
    • 評価指標のmAPには普通IoUが使われるが、GIoUに置き換えてmAPを定義することも可能

    実験

    • YOLOv3( l_2-loss)、FasterRCNN( l_1-loss)、MaskRCNN( l_1-loss)から、regression lossだけIoUやGIoUに置き換えて実験
    • GIoU > IoU > l_n の順で（評価指標は、普通のIoUのmAPでもGIoUのmAPでも）精度が良い
    • two-stage系はRPNのregression lossはそのままで、SubNetworkのregression lossだけ置き換えている
      • 理由は分からない。RPNは後段のSubNetworkでもう1回regressionするので、精度への影響が少ないから？

    感想・コメント

    • 物体検出で、矩形間の「距離」が使われる場面は、評価指標・学習時のregression loss・Anchorへの正解矩形の割り当て の3つ。
      • 単純に考えると、この3つに同じ指標を使った方が良さそう
      • この論文は、評価指標・Lossのみ議論していたが、Anchorへの正解矩形の割り当てには普通IoUが使われるので、LossをIoU系にすればミスマッチはなくなる
      • Box2Pixの論文では、LossとAnchorへの正解矩形の割り当てのミスマッチを解消するために、Lossはそのままで、Anchorへの正解矩形の割り当てに l_2-ノルムを使っている。
    • 一般に、評価指標とLossは必ずしも一致しない
      • Lossは微分可能かつバッチに分離できないといけないため、評価指標をそのままLossに使えない場合が多い
      • この論文で矩形間の距離の定義のミスマッチは解消されたが、評価指標とLossが全く同じになった訳ではない
      • 物体検出の標準的な評価指標であるmAPはバッチごとには計算できず、評価データ全体を使って初めて計算できるので、Lossとしては使えない
      • 一般的な評価指標とLossのミスマッチ対策としては、AppleのLossのメタ強化学習の方法 がある

    参考文献

    *1:社内勉強会で発表した内容を修正して公開した記事になります