こんにちは、CTO室リサーチャーの富田です。 モルフォでは論文紹介を持ち回りで行うジャーナルクラブという活動がありますが、画像処理に関する論文に限らず、担当者が興味を持ったテーマについて紹介することもあります。Google Cloudが昨年公開した COVID-19 感染予測(US版、日本版) は大きな話題になりました。そのホワイトペーパーである "Interpretable Sequence Learning for COVID-19 Forecasting" についてこのジャーナルクラブで発表したので、こちらでもご紹介します。感染者などの時系列推移を学習するだけでなく、疫学の専門家や意思決定者による学習結果の解釈のしやすさを重視した手法となっています。
このホワイトペーパーは機械学習のトップカンファレンスとして知られる NeurIPS 2020 にacceptされていますが、疫学における感染症の数理モデルを大枠としており、意外にも?機械学習的な部分は非常に簡素な作りです。そのため本記事・スライドの前半はその疫学の数理モデルの紹介*1、後半が本論文の手法の紹介となっています。
感染症の数理モデル
感染症は生活習慣病などと違い、病原体への曝露がないと感染しないのが大きな特徴です。人から人へ感染するような感染症では人と完全に接触を断てば感染しないわけですが、現実的にはそれはなかなか難しいものです。そのため感染症の流行はいくつかの仮定を置くことによって、数理モデルによるモデル化が行いやすいという特徴があります。
代表格と言えるのがSIRモデルです。これはあるコミュニティの全人口Nを、
- 感受性人口
(susceptible): 感染症にかかりうる人数
- 感染性人口
(infected): 感染しており、他人に伝染させうる人数
- 治癒人口
(recoverd): 感染から治癒して免疫を獲得した人数
の3つの区画に分け、それらの人数の時間変化を微分方程式でモデル化するものです。IがSへ感染させる割合を表す (感染率)、また感染した人がどれくらいの速さで治癒するかを表す
(治癒率) の2つのパラメータを持ちます。非常に単純なモデルながら、局地的で短期的な流行の様子をよく再現することが知られています[5 §1.1]。
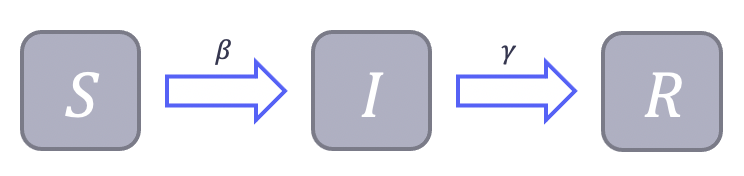
(実際の式などの詳細はスライドや[4,5]などを参照ください。) これを数値的に解いた例が以下のグラフで、感染者数Iが流行初期には指数関数的に増加し、免疫を持たない人の割合が減るにつれてやがて勢いを落とし、最終的にある割合の未感染人口を残して終息するという挙動を見ることができます。
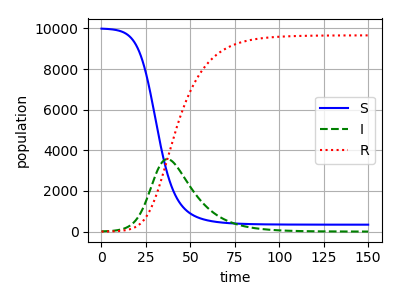
このような感染流行がそもそも発生するかどうかの条件を与える基本再生産数 という量、またどれだけの割合の人がワクチンなどで免疫をもてばこのような流行が発生しないか(集団免疫閾値)、などの量をモデルのパラメータから計算することができます。
このモデルに潜伏期間に対応するEを付け加えたSEIRモデルというものも基本的なモデルとなっており、潜伏期間Eの間は他者へ感染させないという効果を織り込んだものとなっています。現実のデータを解析する際、最近では少なくともSEIR型へ改良したタイプのモデルを用いることが必須となっているようです[5 §2.4]。

SIRモデル、SEIRモデルのような人口を区画に区切った感染症数理モデルはコンパートメントモデルと呼ばれ、感染症数理モデルの基本とも言えるものです[4]。
Googleの感染者数予測モデル
Googleの感染者数予測モデル[1]はSEIRモデルをさらに拡張したものです。例えば感染者のうちでも診断で発見されているかどうかで区分したり、入院状態などを含んだり、再感染の可能性を持つなどしたコンパートメントモデルとなっています。
ただしその内部のパラメータ
などが固定値ではなく、共変量(人の移動量や地域人口など)の関数として表されるようになっています。
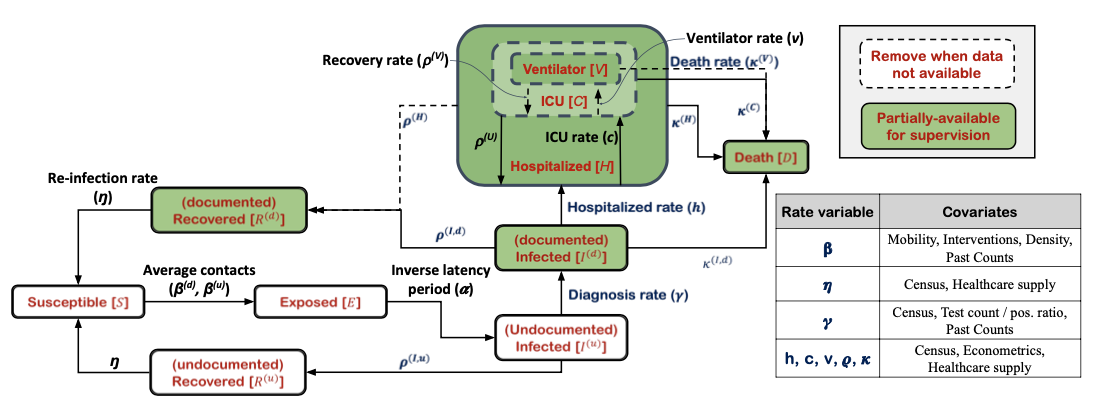
本手法の機械学習部分は、この
- 共変量の時系列予測
- 共変量からパラメータを求める関数の関数形
の2箇所に絞られており、またそれらも非常にシンプルな作りとなっています。 これによって政策決定者や疫学の専門家が学習結果のパラメータなどを調べ、何が感染拡大に寄与しているのかを検討することができるようになっています。
しかしモデルを少しでも柔軟にすると容易にオーバーフィットするなど、様々な苦労があるようです。
詳細は以下のスライドや[1]をご覧ください。
スライド前半で触れている数学セミナー2020年9月号の特集「新型コロナウイルスと闘うために数学にできること」([4])ですが、この特集部分を抜粋したKindle版も販売されているようなので、興味のある方はこの特集タイトルで検索していただくと良いかと思います。また「感染症の数理モデル 増補版」([5])についても最近は在庫が復活したようですので、特集を読んでさらに興味を持った方は見てみるといいのではないでしょうか。
参考文献
- [1] S. O. Arik et al., “Interpretable Sequence Learning for COVID-19 Forecasting,” arXiv:2008.00646 [cs, stat], Aug. 2020. http://arxiv.org/abs/2008.00646
- [2] Z. Qian, A. M. Alaa, and M. van der Schaar, “When and How to Lift the Lockdown? Global COVID- 19 Scenario Analysis and Policy Assessment using Compartmental Gaussian Processes,” arXiv:2005.08837 [physics, stat], Jun. 2020. http://arxiv.org/abs/2005.08837
- [3] E. Drysdale, D. Singh, and A. Goldenberg, “Forecasting Emergency Department Capacity Constraints for COVID Isolation Beds,” arXiv:2011.06058 [cs], Nov. 2020. http://arxiv.org/abs/2011.06058
- [4] 数学セミナー2020年9月号. 日本評論社, 2020.
- [5] 稲葉寿, 感染症の数理モデル, 増補版. 東京: 培風館, 2020.
*1:この部分についてはなるべく元の文献に沿う形にした上で他の文献にもいくつか当たるなどして正確を期す努力はしていますが、私は疫学のバックグラウンドはない(物理が専門でした)ことをお断りしておきます。